2023年のアクチュアリー試験まであと数か月となり、受験生におかれましては、そろそろラストスパートに突入される時期かと存じます。
また、昨年からCBTによる試験がスタートしていますので、特に初受験の方は是非、体験版(http://it.prometric-jp.com/tutorial/actuaries/first_stage_exam/index.html)で、操作方法などを事前にチェックしておきたいですね。
そこで、今回のコラムでは、アクチュアリー試験のうち「第1次試験(生保数理)」について、重要性が高いと考えられる論点を幾つかご紹介いたしましょう。
なお、当コラムに関連する過去のコラム(https://www.vrp-p.jp/acpedia/3677/、https://www.vrp-p.jp/acpedia/3162/、https://www.vrp-p.jp/acpedia/2366/)も併せてご覧いただけますと幸いです。
1.教科書にない公式
以下の2つの公式は、就業者が就業不能者になった後の生存(残存)確率を表します。
これらのうち、(1)は教科書(下巻)158ページ(13.1.19)に登場しますが、(2)は教科書に登場しません。
(1)
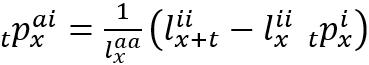
(2)
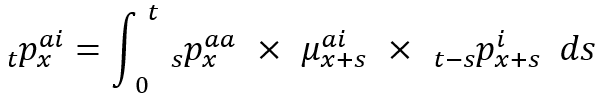
しかし、過去問では、平成16年度問題1(7)、平成9年度(保険数学2)問題4(1)、平成7年度(保険数学2)問題1(5)などで(2)の公式が登場します。
なお、アクチュアリー試験の資格試験要領によれば、第1次試験(基礎科目)の出題範囲は教科書に限定されるため、教科書に登場しない公式を用いることは同要領に反するのでは?と思われるかもしれません。
実は、教科書(下巻)「第12章連合生命に関する生命保険および年金」に登場するモデルおよび公式を応用すれば、(2)の公式を導くことも可能です。
古いコラムで恐縮ですが、「教科書にない公式(生保数理編)2016年3月24日 (木)」も是非ご覧いただければ幸いです。
2.付加保険料が予定新契約費のみ
例えば、2021年度問題2(5)のように、営業保険料を求める問題で、“予定事業費は予定新契約費のみ”という条件が与えられることも少なくありません。
さらに、大抵の場合、当該条件を伴う場合、チルメル式責任準備金と絡めた出題が多いことも特徴です。
これは、チルメル式責任準備金で登場する2つの純保険料(P1, P2)のうち、特に、P2の方がチルメル割合(α)を伴う形で表示されますが、このαを(チルメル割合ではなく)予定事業費と考えれば、“純保険料+付加保険料(=予定新契約費)”という形で表示されているとも解釈されることに由来しています。
なお、問題文に、“予定事業費は予定新契約費のみ”および“チルメル式責任準備金”という表現があれば、ほぼ間違いなく、2021年度問題2(5)と同じように解けますので、「切り札」の1つとして是非、習得しておきたいですね。
3.生存者総数に占める就業不能者数の割合
上記の2.と同様に、問題文に“生存者総数に占める就業不能者数の割合”という表現が登場した場合、教科書(下巻)160ページ(13.1.27)
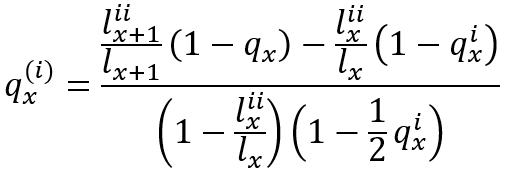
のうち、「![]() 」および「
」および「![]() 」が当該割合となります。
」が当該割合となります。
なお、上記の公式は試験テクニックとしてだけではなく、実務上でも非常に重要な公式でして、就業不能保障保険はもちろんのこと、がん保険などの生前給付型保険において、統計的に直接求めることが難しい「![]() 」を、統計的に求め易い「
」を、統計的に求め易い「![]() 」および「
」および「![]() 」を用いて計算することで、当該保険の営業保険料などを求めることが可能となります。
」を用いて計算することで、当該保険の営業保険料などを求めることが可能となります。
4.経済価値ベース
2025年度決算で導入予定の“経済価値ベースのソルベンシー規制”に向けて、FT(フィールドテスト)仕様書の改定並びに金融庁専用サイトの拡充が益々進展していますね。
当該規制をアクチュアリー試験範囲に照らせば、保険2(生命保険、損害保険)が筆頭に挙がりますが、生保数理も無関係ではありません。
実際、保険料計算基礎率と実績基礎率(例.経験死亡率など)との関係では、いわゆる“BE(ベスト・エスティメイト=最良推計)”に基づく将来キャッシュフローが必要不可欠であり、生保数理の教科書(上巻)「第6章計算基礎の変更」を中心に、予定死亡率などの計算基礎率を変更した場合の保険料および責任準備金などの保険価格の動きに関する出題が考えられます。
このため、例えば、平成26年度問題3のような、責任準備金の再帰式を辺々引いた場合の計算テクニック(例.同じ項を引いて加えるなど)も併せてチェックしておくとよいでしょう。
いかがでしたか。昨年のコラムでも触れましたが、アクチュアリー試験は直前になればなるほど、緊張感のために、なかなか集中できない日々が続く可能性もあります。今回ご紹介した内容をしっかりと押さえた上で、良い結果につながることを祈念しております。
(ペンネーム:活用算方)







