今年もアクチュアリー試験が近付いてきましたが、受験生の皆さまにおかれましては、いよいよラストスパートに突入されているかと存じます。

また、新型コロナウイルスのワクチン接種がかなり進みましたが、同ウイルス蔓延の終息は依然として不透明であり、試験運営はもちろん、各社の商品戦略やアクチュアリー試験の出題傾向にも、まだまだ大きな影響を持っているようにも思われます。

そこで、今回のコラムでは、昨年10月のコラム（https://www.vrp-p.jp/acpedia/2366/）と同様に、アクチュアリー試験の第１次試験（生保数理）について、特に重要と考えられる論点を幾つかご紹介いたします。

１．全期（その１）

生保数理では、『全期』と呼ばれる条件が２つ登場します。具体的には、n=mおよびh=mです。
ここで、n=mとは、保険期間と保険料払込期間が等しいことを表し、保険料全期払込とも呼ばれます。なお、教科書の練習問題や過去問など、生保数理に関する問題設定では、この条件が頻繁に登場します。

特に、頻出公式である、教科書（上巻）178ページ（5.3.7）は、n=mであることが前提です。したがって、例えば、10年満期の養老保険で保険料払込期間が5年の場合、当該公式は成り立たないことに注意しましょう。

２．全期（その２）

一方、h=mとは、チルメル期間と保険料払込期間が等しいことを表し、全期チルメル式とも呼ばれます。
なお、初学者の方は、１．のn=mという条件に惑わされて、h=nが全期チルメル式と誤解しやすいので注意しましょう。したがって、例えば、10年満期の養老保険で保険料払込期間が5年の場合、全期チルメル式といえば、チルメル期間が（10年ではなく）5年となります。

特に、チルメル式責任準備金のうち頻出問題である『初年度定期式責任準備金』は、教科書（下巻）12ページの7～8行目にかけて記載の通り、全期チルメル式責任準備金、つまり、h=mであることも条件に含まれますので、しっかりと押さえておきましょう。

３．責任準備金の再帰式の変形（その１）

責任準備金の再帰式に関する出題パターンとしては、例えば、
１）責任準備金を計算
２）純保険料を計算
３）２種類の計算基礎率に基づく２つの再帰式から差分（Δqなど）を計算
といったものが挙げられます。

このうち、３）については、2020年問題2(4)で（予定利率を変えずに）予定死亡率のみを変えた場合が出題されました。
なお、予定死亡率と予定利率を同時変更した場合、責任準備金の再帰式を辺々引いて変形すれば、下図のような結果（守田常直氏（保険数学）下巻265ページ）が得られますので、是非、変形にチャレンジしてみてください。

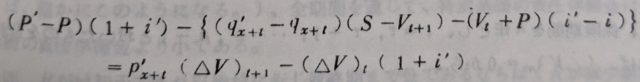
４．責任準備金の再帰式の変形（その２）

生保数理の難問として有名な、平成21年度問題3(2)では、責任準備金の差分（ΔV）の符号が『一度だけ』変わる事例です。
一方、日本アクチュアリー会の会報別冊第88号『計算基礎の変更と保険関数－Moserの定理をめぐって－1984年2月』の41ページ（資料上は38ページ）にある『4－3責任準備金差額の符号が2度変る例』では、ΔVの符号が『二度』変わる例が紹介されています。

生保数理が易化傾向でしたので、今年は難問が出題されるかもしれませんね。

いかがでしたか。昨年のコラムでも触れましたが、アクチュアリー試験は直前になればなるほど、緊張感からか、なかなか集中できない日々が続く可能性もあります。今回ご紹介した内容をしっかりと押さえ、良い結果につながることを祈念しております。

（ペンネーム：活用算方）