2020年の出来事として『コロナウイルスの蔓延』は後世に語り継がれると思いますが、アクチュアリーにとっても、同ウイルスによる死亡を『災害死亡保険金の支払対象』とするのか、さらに、普通保険約款の支払事由に明記されなくても、『柔軟な解釈』で遡及して支払対象とするのか、といったかつてない状況に直面した年とも言えます。
一方、アクチュアリーの専門領域である『保険数理の世界』を拡大して、『一般的な数学の世界』における2020年の歴史的イベントとしては、何と言っても、京都大学の望月新一教授によるABC予想の解決が挙げられるでしょう。
日本アクチュアリー会ホームページ(http://www.actuaries.jp/examin/faq.html#link06)によれば、資格取得者の平均受験年数は、準会員が約5年、正会員が約8年ですが、ABC予想証明に係る望月教授の論文査読も約8年(2012年:ホームページで公開、2020年:査読終了)かかったそうです。
数学の証明もアクチュアリー正会員に至るのも、長い道のりですね。。。
そこで、今回のコラムでは、ABC予想をはじめとする『良い予想』とは何かを考察しながら、歴史的に有名な『リーマン予想』について、アクチュアリーの視点から思うところを述べてみましょう。
1.良い予想とは
古来多くの『予想』が数学界では登場してきましたが、その度に、新たな『道具』が開発されてきました。そして、その予想を解く過程において様々な『数学的副産物』が産み出され、場合によっては、予想そのものよりもそれらの副産物の方が価値が高く、結果的に数学をさらに発展させる原動力となったものも少なくないと思われます。
そもそも、良い予想とは何でしょうか?筆者は少なくとも以下の3つの性質を満たすものが良い予想であると考えます。
(1)予想の内容が分かり易いものであること
(2)その予想が解決すれば既存の別の予想が証明されること
(3)その予想を解決する過程が数学の発展に寄与すること
これらの性質は、数学の世界だけでなく、アクチュアリーを含む普段の仕事にも通じる面があります。実際、上司が部下に業務を指示する場合、
(1)指示内容が分かり易いものであること
(2)指示内容が解決すれば既存の別の業務が効率化されること
(3)指示内容を解決する過程が業務の発展に寄与すること
という面があれば理想的な業務指示と言えるでしょう。
なお、(3)の業務の発展には、当然、部下の育成も含まれますので、様々な予想に挑んで数学者としての資質向上を図るのと同様、本人の成長に丁度良いレベルの仕事を与えて、部下の人材育成や問題解決能力等を向上させることは、まさに、重要なOJTといえるでしょう。
2.ABC予想からフェルマー予想へ
ABC予想の最も有名な性質かもしれませんが、『ABC予想』から『フェルマーの最終定理』が以下の手順で導かれます。
手順1) ABC予想が正しい。
手順2) 全ての互いに素な正整数の組(a,b,c)でa+b=cであるものに対し、
c<rad(abc)^2が成立。(←rad(x)は整数xの正の素因数の積、a^bはaのb乗)
手順3) ある互いに素な正整数の組(x,y,z)が存在し、自然数n≥3 に対しx^n+y^n=z^n を満たす。(一般性を失うことなく、0 < x < y < z と仮定してよい。)
手順4) 手順2)および手順3)より、z^n < rad(x^n×y^n×z^n)^2となるが、一般に、整数kに対してrad(k^n) = rad(k) ≤ kとなるため、
z^n < rad(x^n×y^n×z^n)^2 ≤ (x×y×z)^2 < (z×z×z)^2 = z^6
手順5) 0 < zおよび手順4)より、n < 6 となるので、n = 3,4,5。
手順6) 一方、n = 3,4,5の場合、正整数の組(x,y,z)でx^n+y^n=z^n を満たすものは存在しないことが既に証明済み。
上記の証明は、https://mikan-alpha.hatenablog.com/entry/abc-to-fermatから引用させていただきましたが、証明は極めて平易で、小学生でも理解できますね。
なお、『フェルマーの最終定理』自体は1995年に半安定な楕円曲線に関する『志村-谷山-Weil予想』から既に導かれていますが、ここでも日本人数学者である志村五郎氏、谷山豊氏が登場するあたりが、筆者が代数的整数論を志して本当に良かったと心から指導教官に感謝しています。
A.Wiles教授による証明の第一報が世界中を駆け巡った当時、私は生命保険会社から無事内定を頂けたのですが、指導教官が寂しそうな表情で『Fermat予想が解決されてしまったので(君を含めて)整数論を諦める学生が多くなりそうだね。。。』と呟かれたのが、とても申し訳なかったです。
3.アクチュアリーとリーマン予想
日本アクチュアリー会ホームページの会員サイトにある『ライブラリー』から、カテゴリトップ » 会報別冊 » 第213号 変額年金保険等の最低保証リスクに係る責任準備金の積立等について、の順に進んでいただくと、最低保証リスクに係る責任準備金の積立に関する公式が登場します。
特に、同別冊の33ページには、『資産価格の最大値の評価を、離散的(年1回など)にしか行わない場合』の支出現価を表す数式として、
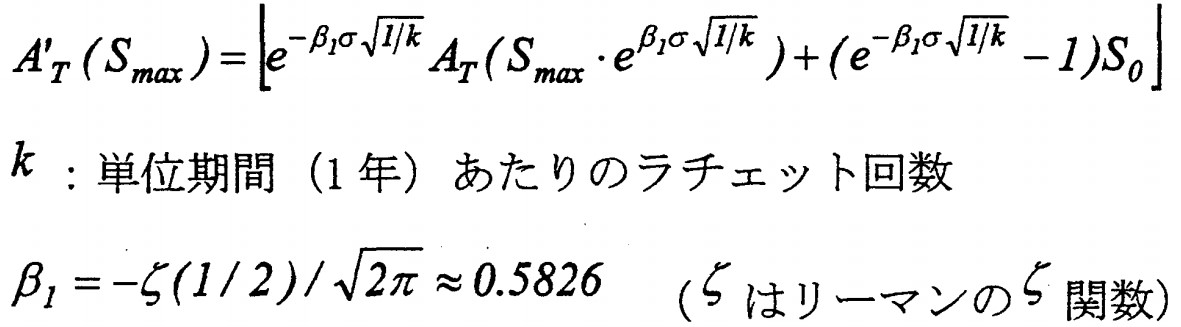
が紹介されているのですが、特に注目すべき点は、リーマンのζ(ゼータ)関数ζ(s)のs=1/2 での値が登場するところです。
通常、(実函数としての)ζ関数は、s > 1 の範囲で『無限級数』で定義され、例えば、ζ(2) = π^2/6 のように、ベルヌイ数との関係性も知られています。また、有名な『リーマン予想』は『(複素関数としての)ζ関数の非自明な零点の実部は1/2 に限られることを主張しています。
このような状況で、-ζ(1/2) が登場することは極めて驚くべきことでして、最低保証付きの変額年金保険という、アクチュアリーにとって重要な保険種類に関して、一般的な数学の世界との接点が見いだせることは、非常に素晴らしいことだと思います。
4.確率・統計入門の『余白』
小針 晛宏(こはり あきひろ)氏が執筆された『確率・統計入門(岩波書店)』は、私が大学の確率統計の授業と格闘していた時、とても参考になった数学書です。残念ながら、当時、小針氏は既に『鬼籍』に入られ、フィールズ賞受賞者である広中平祐氏の『序にかえて』は、ある種の『弔文』と位置付けられるのですが、132ページの余白に書きとめられた、

の、なんとも言えない『ほのぼのとした雰囲気』は、恐らく多くの数学者たちを魅了したことでしょうし、広中氏の暖かい文章は、当時、大学生であった筆者の心を大いに揺さぶりました。
恰も、『この定理に関して、私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。』と書き遺したPierre de Fermat に通じるものがあります。
『エネルギー保存の法則』は反例が見つからないため、一応、『正しい』と認められていると、高校時代に物理の先生から教えていただいた記憶があるのですが、ABC予想やリーマン予想も、ある種、自然界の法則に導かれる形で証明されるのではないかと日々、考えを巡らせています。
いかがでしたか。このコラムのタイトルにある『新リーマン予想』は、『新(=サラ)』と読めば、『サラ・リーマン予想』とも読めます。サラリーマン(近年はサラリーパーソンと呼称すべきですね)ならではの、実務面からの証明可能性(例.複素関数としてのリーマンのゼータ函数の非自明ゼロ点の実部は、株式投資の勝敗が均衡になる確率に等しいことから、1/2を導く)を追究したいものです。
上述の望月教授の誕生日は(1969年)3月29日で、丁度、筆者の4か月先輩です。そして、(2020年)3月29日は、日本を代表するコメディアンである志村けん氏の命日です。コロナウイルスとABC予想にどのような関係があるか分かりませんが、フェルマー予想で登場する志村(五郎)氏と奇しくも同じ苗字である点など、単なる偶然とは思えない気がしてなりません。
(ペンネーム:活用算方)