定常状態（定常社会）開集団は、日本アクチュアリー会資格試験のうち『生保数理』の頻出論点ですが、営業保険料や責任準備金等の主要論点に直接関係なく、実務上の活用機会も多くないことから、その概念やモデルを具体的な数式で表示することを不得手とする受験生が少なくないように思えます。

そこで、今回のコラムでは、日本年金数理人会能力判定試験のうち、2019年度年金数理問題３を教材にして、定常状態を数式で表すテクニックをご紹介いたします。

なお、同試験の解答が同会から公開されておりますが、日本アクチュアリー会資格試験と異なり、解答の流れは公開されていないため、以下の解答例は筆者のオリジナルである点を予めお断りしておきます。（もちろん、解答の結論が正しいことを同会の公式解答と一致することは確認済みです）

１．藤田先生からの貴重なアドバイス

モデリングの教科書等の著者である藤田岳彦先生の資料（※１）は、アクチュアリー試験受験生必読の資料と言われていますが、当資料に限らず先生の書籍（例．『解いて分かるガロア理論（東京書籍）』（※２）など）は、軽妙な語り口で初心者・上級者を問わず、その分かり易さに定評があります。

幸い、筆者は、藤田先生と懇親会で同じテーブルに座る機会を得ましたが、中でも、『高木貞治氏の解析概論を小学生の時に読破した。』というコメントには参りました。（私も一応、理学部数学科出身ですが、大学の教養学部時代に解析概論を理解するのがやっとという状況でした（泣））

特に、『部分積分は負け』という先生のご指摘は、数学に限らず、生保数理や年金数理にも応用できる積分変形テクニックですので、藤田先生の造詣の深さには脱帽です。

※１　http://www.olis.or.jp/hfea/pdf/20130126forum_fujita.pdf（２６ページ）

※２　ご本人からサインをいただけました。

２．解答例

上述の通り、能力判定試験の公式解答（※３）は解答のみが公開され、解答に至る流れは非公開となっておりますので、独自の解答案を以下に記載いたします。

※３　http://www.jscpa.or.jp/become/test/past/index.html（２６ページ）

《解答例》

定常状態崩壊後から30年が経過した場合：

0歳の生存者数（＝出生者数）：\(e^{-0.05\times30}\times\ l_0\)

1歳の生存者数：\(e^{-0.05\times\left(30-1\right)}\times\ l_{0+1}\)

2歳の生存者数：\(e^{-0.05\times\left(30-2\right)}\times\ l_{0+2}\)

・・・

x歳の生存者数：\(e^{-0.05\times\left(30-x\right)}\times\ l_{0+x}\)

したがって、定常状態崩壊後から30年が経過した場合の生存者総数は、
\[\int_{0}^{30}{e^{-0.05\times\left(30-x\right)}l_x^\ dx}\]
よって、求める平均年齢は、
\[\frac{\int_{0}^{30}{xe^{-0.05\times\left(30-x\right)}l_x^\ dx}}{\int_{0}^{30}{e^{-0.05\times\left(30-x\right)}l_x^\ dx}}=\frac{\int_{0}^{30}{xe^{-0.05\times30}e^{0.05x}l_x^\ dx}}{\int_{0}^{30}{e^{-0.05\times30}e^{0.05x}l_x^\ dx}}=\frac{e^{-0.05\times30}\int_{0}^{30}{xe^{0.05x}l_x^\ dx}}{e^{-0.05\times30}\int_{0}^{30}{e^{0.05x}l_x^\ dx}}=\frac{\int_{0}^{30}{xe^{0.05x}l_x^\ dx}}{\int_{0}^{30}{e^{0.05x}l_x^\ dx}}\]

（分母）＝\(\int_{0}^{30}{e^{0.05x}l_x^\ dx}=\int_{0}^{30}{e^{0.05x}l_0^\ \left(1-e^{-0.2\left(30-x\right)}\right)dx}\)
\[=l_0^\ \int_{0}^{30}{e^{0.05x}\left(1-e^{-\left(6-0.2x\right)}\right)dx}=l_0^\ \int_{0}^{30}{e^{0.05x}-e^{-\left(6-0.25x\right)}dx}\]

\[=l_0^\ \times\left\{\left[\frac{e^{0.05x}}{0.05}\right]_0^{30}-\left[\frac{e^{-\left(6-0.25x\right)}}{0.25}\right]_0^{30}\right\}=l_0^ \times\left(\frac{e^{1.5}-1}{0.05}-\frac{e^{1.5}-e^{-6}}{0.25}\right)\]
\[=l_0^\ \times\left(\frac{\sqrt{e^3}-1}{0.05}-\frac{\sqrt{e^3}-\frac{1}{\left(e^3\right)^2}}{0.25}\right)=l_0^\ \times\left(\frac{\sqrt{20.085537}-1}{0.05}-\frac{\sqrt{20.085537}-\frac{1}{\left(20.085537\right)^2}}{0.25}\right)\]
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \fallingdotseq\ l_0^\ \times51.716940\)*

* 30を超えたため、計算間違いに見えるかもしれませんが、上記変形において、\(e^{-0.05\times30}\)を分子分母でキャンセルしているため、キャンセル前の（分母）としては、\(e^{-0.05\times30}=e^{-1.5}=\frac{1}{\sqrt{e^3}}=\frac{1}{\sqrt{20.085537}}\fallingdotseq\frac{1}{4.4816891}\fallingdotseq0.223130\)を乗じる必要があります。この結果、\(l_0^\ \times11.54\)が分母の値となります。

（分子）＝\(\int_{0}^{30}{xe^{0.05x}l_x^\ dx}=\int_{0}^{30}{{xe}^{0.05x}l_0^\ \left(1-e^{-0.2\left(30-x\right)}\right)dx}\)
\[=l_0^\ \int_{0}^{30}{xe^{0.05x}\left(1-e^{-\left(6-0.2x\right)}\right)dx}=l_0^\ \int_{0}^{30}{xe^{0.05x}-xe^{-\left(6-0.25x\right)}dx}\]
\[=l_0^\ \times\left\{\int_{0}^{30}{xe^{0.05x}dx}-l_0^\ \int_{0}^{30}{xe^{-\left(6-0.25x\right)}dx}\right\}\]

ここで、

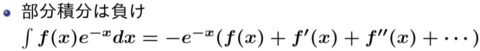
より、\(0.05x=-y\)とおけば、\(x:0\rightarrow30\ \)のとき、\(y:0\rightarrow-1.5\)であり、\(\frac{dx}{dy}=\frac{d}{dy}\frac{-y}{0.05}=\frac{-1}{0.05}\)　となるので、
\[\int_{0}^{30}{xe^{0.05x}dx}=\int_{0}^{-1.5}{\frac{1}{{0.05}^2}ye^{-y}dy}=400\int_{0}^{-1.5}{ye^{-y}dy}=400\left[-e^{-y}\left(y+1\right)\right]_0^{-1.5}\]
同様に、\(6-0.25x=y\)とおけば、\(x:0\rightarrow30\)のとき、\(\ y:6\rightarrow-1.5\)であり、\(\frac{dx}{dy}=\frac{d}{dy}\frac{6-y}{0.25}=\frac{-1}{0.25}\)　となるので、
\[\int_{0}^{30}{xe^{-\left(6-0.25x\right)}dx}=\int_{6}^{-1.5}{\frac{y-6}{{0.25}^2}e^{-y}dy}=\frac{1}{{0.25}^2}\int_{6}^{-1.5}{\left(y-6\right)e^{-y}dy}\]
\[=16\int_{6}^{-1.5}{ye^{-y}-6e^{-y}dy}=16\int_{6}^{-1.5}{ye^{-y}dy}-96\int_{6}^{-1.5}{e^{-y}dy}\]
\[=16\left[-e^{-y}\left(y+1\right)\right]_6^{-1.5}-96\left[-e^{-y}\right]_6^{-1.5}\]
\[=16\left({0.5e}^{1.5}+{7e}^{-6}\right)-96\left(-e^{1.5}+e^{-6}\right)={104e}^{1.5}-16e^{-6}\]
よって、

（分子）\(=l_0^\ \times\left\{\int_{0}^{30}{xe^{0.05x}dx}-l_0^\ \int_{0}^{30}{xe^{-\left(6-0.25x\right)}dx}\right\}=l_0^\ \times\left\{400\times\left({0.5e}^{1.5}+1\right)-\left({104e}^{1.5}-16e^{-6}\right)\right\}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =l_0^\ \times\left({96e}^{1.5}+400+16e^{-6}\right)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =l_0^\ \times\left(96\sqrt{e^3}+400+16\frac{1}{\left(e^3\right)^2}\right)=l_0^\ \times\left(96\sqrt{20.085537}+400+16\frac{1}{\left(20.085537\right)^2}\right)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \fallingdotseq\ l_0^\ \times830.281812\)

ゆえに、求める平均年齢は、

\(\frac{\int_{0}^{30}{xe^{-0.05\times\left(30-x\right)}l_x^\ dx}}{\int_{0}^{30}{e^{-0.05\times\left(30-x\right)}l_x^\ dx}}=\frac{830.281812}{51.716940}\fallingdotseq16.054349\)

（答）（Ｂ）

補則：仮に、定常状態崩壊後から50年が経過した場合の生存者総数を考えても、
\[\int_{0}^{30}{e^{-0.05\times\left(50-x\right)}l_x^\ dx}\]
となり、被積分関数の『50にかかる部分』は分子・分母でキャンセルされ、答えに影響を与えません。（解答終）

３．問題文の訂正

この問題の問題文では、\(l_x＝l01-e-0.230-x\) という条件が与えられているのですが、xに0を代入すると、\(e^{-6}=0\) が成立しなければならず不整合になりますので、同会から訂正記事が公表されています。（※４）

※４　http://www.jscpa.or.jp/become/test/pdf/2019/nensuu_renraku.pdf

能力判定試験の採点基準は不明ですが、日本アクチュアリー会資格試験の場合には、このような不備が発生した場合は、受験生全員に得点が与えられることもありますので、逆に、全員への得点付与を期待する余り、得点が獲得できないという事態にもなりかねません。

受験生にとっては、もちろん、不備のない出題を期待したいところですが、問題作成者も同じ人間である以上、このようなヒューマンエラーは不可避かもしれません。

いずれにせよ、『全員得点』という淡い期待を抱くことなく、かつ、問題文の『空気』を読みながら、解答に専念できるようになりたいものです。

いかがでしたか。日本アクチュアリー会資格試験の『生保数理』と、能力判定試験の『基礎数理Ⅱ』の問題が類似しているため、生保数理の受験生は基礎数理Ⅱに挑むケースが多いようにも思えますが、是非、能力判定試験の『年金数理』にも挑戦していただければ、より実力が定着するのではないかと思います。

新型コロナウイルスの収束がまだまだ不透明ですが、受験生の皆さまにおかれましては、手洗い・うがい・マスクをしながら、アクチュアリー試験の勉強が順調に進むことを祈念いたしております。

（ペンネーム：活用算方）