新型コロナウイルスの影響で在宅勤務を余儀なくされている社会人も多いかと思いますが、通勤時間が省略できて、『アクチュアリー試験勉強時間が確保できた！』という受験生の声を多く聞いたりもします。

そこで、今回のコラムでは、自宅で勉強されている受験生に向けて、アクチュアリー試験のうち、特に生保数理について、教科書だけでは理解が難しいと思われる過去問をご紹介いたしょう。

具体的には、平成７年度（保険数学１）問題１（２）でして、
『定常人口社会で、lx = a－x（0≦x≦a）、かつ、30歳以上の人の死亡時年齢の平均が75歳のとき、aを求めよ？』
という問題です。（←表示の都合上、問題文を一部修正。）

直感的には、
・生存者数が直線的に減少
・30歳の人の平均余命が45年（＝75歳－30歳）
という２つの条件から、最終年齢aは、a = 30 + 45 + 45 = 120歳で計算できると思われるかもしれませんが、120歳が選択肢にないため、この計算は誤りとなります。

では、問題文をどのように解釈すればよいのでしょうか？

恐らく、混乱を来す表現は、『30歳以上の人の死亡時年齢の平均』だと思われます。実際、平成14年度（生保数理）問題２（１）でも、
『定常社会で（中略）60歳以上で死亡する者の平均年齢が70歳』
という表現が登場します。

これらの問題を少し変形して並べてみると、
『定常社会で30歳以上の人の死亡時年齢の平均が75歳』
『定常社会で60歳以上で死亡する者の平均年齢が70歳』
となり、日本語としては同じような表現にも見えるのですが、解法は全く異なります！

実際、両者の公式解答を比較してみると、

『定常社会で30歳以上の人の死亡時年齢の平均』

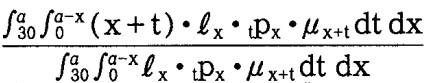
『定常社会で60歳以上で死亡する者の平均年齢』

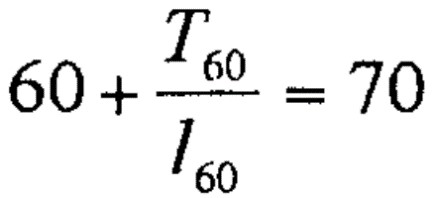
となります。

あえて、試験委員の味方（見方）をすれば、生保数理において、
『死亡時の平均年齢』
は、定常状態（定常社会）の場合、
『死亡者の年齢の加重平均値』
として定まるのですが、一方で、
『XX歳以上（で死亡する者）』
の定義は、（少なくとも）二つあるよ、ということです。

実際、下図をご覧いただければ、平成７年度の問題では、下図のうち斜線部分（面の概念）をスタート時点の『生存者』と捉えているのに対し、平成14年度の問題では、下図のうち太線部分（線の概念）をスタート時点の『生存者』と捉えているようです。

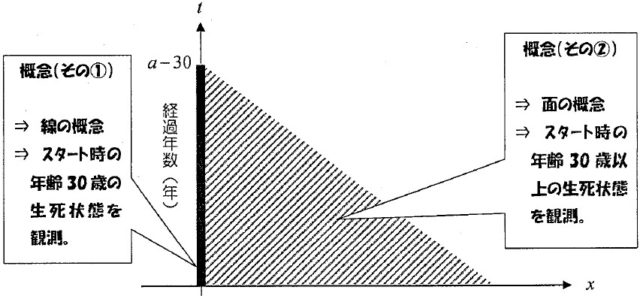
したがって、図形的な観点から考察すれば、平成７年度の問題では、上図の斜線部分を底面とするような『三角錐』を十分時間が経過した場合の全人口と捉えているのに対して、平成14年度の問題では、上図の太線部分をスタート時点の全人口と捉えて、斜線部分を含めた三角形を十分時間が経過した場合の全人口として捉えていることがお分かりいただけると思います。

このように、アクチュアリー試験では、問題文における日本語としての『意味』を正しく解釈することも『基礎的知識』に含まれているようです。

いかがでしたか。資格試験要領に明記されている通り、アクチュアリー試験のうち第１次試験（基礎科目）の出題範囲は教科書に限定されていますが、その一方で、教科書に掲載されていない解法も過去問で学習しなければ満点が獲得できないのも事実です。
今回のコラムが少しでも受験生の一助となれば幸いです。

（ペンネーム：活用算方）