2018年度の生保数理問題1(1)の公式解答で、

\((Ia)_{\overline{\small{\ n\ }|}}=\frac{1}{d}\cdot a_{\overline{\small{\ n\ }|}}-\frac{n\ \cdot\ v^n}{i}\)

という公式が登場します。

　これは、教科書（上巻）21ページ（1.8.4）と同じ式であり、その導き方も教科書（上巻）20ページで紹介されていますが、試験本番で下書き用紙等を用いて最初からこの公式を導く時間的余裕はないでしょうから、試験対策としては丸暗記するしかないと諦める受験生も少なくないと思われます。

　そこで、今回のコラムでは、『ブロック図』という手法を用いて、この公式を視覚的に導く方法をご紹介したいと思います。

１．有限＝無限－無限
　生保数理に登場する数学的テクニックの１つとして、『有限＝無限－無限』という関係、つまり、『無限同士の差で有限を表す』があります。しかし、上記の公式をみた場合、右辺の差分が『無限同士の差』ではなく『有限同士の差』と思われるかもしれません。

２．永久年金とは
　上記の公式の右辺に登場する、『dの逆数（＝1/d）』および『iの逆数（＝1/i）』は、永久年金（＝支払が永久に続く年金）現価と等しいもので、それぞれ、『dの逆数』が期始払を、また、『iの逆数』が期末払の年金現価を表します。
つまり、数学的に、dで割ったり、iで割ったりすることは、（期始払および期末払の）永久年金現価を乗じることと等しくなるのです。

３．ブロック図とは
　いよいよ本題に入りましょう。上記の公式の左辺は『n年満期の期末払累加年金現価』を表しますが、ブロック図を描く場合、『縦軸が年金額』、『横軸が時間の経過』を表すとして、以下の3点に注目します。
《注目１》n年満期　←　ブロック図の底辺がn個
《注目２》期末払　　←　１つのブロックの右側の縦線で年金を支払う
《注目３》累加年金　←　ブロックが1段ずつ積み上がる（年金額が毎年１増える）

　例えば、n=3の場合、上記の公式の左辺に対応するブロック図は以下の通りです。

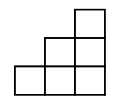
　念のため、ブロック図の見方を説明しますと、一番左にある１つのブロックが1回目の年金『v』に対応します。また、一番右側の3階建てになっているブロックが3回目の年金『3×v^3（vの3乗の3倍）』に対応します。

４．永久年金のブロック図
　上記３．のブロック図が公式の左辺の年金現価を表しますが、公式の右辺の年金現価をブロック図で表すとどうなるでしょうか。
　先ほどと同様、n=3の場合、公式全体を描いてみれば以下のようになります。

　念のため、ブロック図の見方を説明しますと、黄色のブロックから赤いブロックを引いた残りが上記の公式の左辺に対応します。
　それでは、黄色のブロックおよび赤いブロックそのものは、どのようにして計算すれば良いのでしょうか？
それには、平行四辺形の面積の公式『底辺×高さ』を用いれば良いのです。
　まず、黄色のブロックから考えると、『底辺』は横に3個つながったブロックで、『高さ』は縦に伸びる（期始払の）永久年金現価となります。なお、『底辺』がすでに期末払となっているため、縦に伸びる永久年金現価は期始払となります。つまり、

黄色のブロック＝『底辺』×『高さ』＝\(a_{\overline{\small{\ 3\ }|}}\times\frac{1}{d}\)

となります。
　次に、赤色のブロックを考えると、黄色のブロックと縦横を入れ替えて、赤いブロックの一番左にある縦（横ではありません）に3個つながったブロックを『底辺』と考えて、『高さ』は横（縦ではありません）に伸びる（期始払の）永久年金現価となります。なお、『底辺』がすでに期末払となっているため、縦に伸びる永久年金現価が期始払となる点は黄色のブロックと同じです。つまり、

赤色のブロック＝『底辺』×『高さ』＝\((3\times v^4)\times\frac{1}{d}=\frac{3\times v^4}{d}=\frac{3\times v^4}{iv}=\frac{3\times v^3}{i}\)

となります。なお、最後から2つ目の“＝”では、分母に“ダイブの公式（\(d=iv\)）”を用いている点に注意してください。

　以上の結果、n=3の場合、

公式の左辺＝（黄色のブロック）－（赤色のブロック）＝\(a_{\overline{\small{\ 3\ }|}}\times\frac{1}{d}-\frac{3\times v^3}{i}\)

となりますので、これが最初にご覧いただいた公式（のn=3の場合）となります。

いかがでしたか。生保数理に限らず、アクチュアリー試験を突破するためには、ある程度の『丸暗記』は避けて通れません。しかし、大量の公式を丸暗記できるほど時間的余裕はないでしょうから、今回ご紹介した図形的な意味から公式を導くテクニックも身に着けることが、早期合格の秘訣といえるでしょう。（ペンネーム：活用算方）